集训之数学专题
A
题目简介
求
$$
f(n) = (\prod_{i = 1}^{n}\prod_{j|i}\prod_{k|j}(1 + \dfrac{1}{k})) \bmod 998244353
$$
的值。
题目分析
先交换尝试交换次序
先将 $i$ 交换到最后面,得到
$$
f(n) = \prod_{j = 1}^n\prod_{k|j}(1 + \dfrac{1}{k})^{\lfloor\frac{n}{j}\rfloor}
$$
同理,如果令 $j = tk$,将 $j$ 交换到最后面,得到
$$
\begin{split}f(n)
&= \prod_{k = 1}^{n}\prod_{t = 1}^{\lfloor\frac{n}{k}\rfloor}(1 + \dfrac{1}{k})^{\lfloor\frac{n}{tk}\rfloor}\
&= \prod_{k = 1}(1 + \dfrac{1}{k})^{\sum_{t = 1}^{\lfloor\frac{n}{k}\rfloor}\lfloor\frac{n}{tk}\rfloor}\
&= \prod_{k = 1}(\dfrac{1 + k}{k})^{\sum_{t = 1}^{\lfloor\frac{n}{k}\rfloor}\lfloor\frac{n}{tk}\rfloor}
\end{split}
$$
现在即是一个两次嵌套整除分块的形式,但现在考虑处理乘积,因为 $n$ 太大,不能前缀积,但底数显然是一个列项相消的形式,考虑外层整除分块计算 $l \sim r$ 时,可以裂项相消变为 $\dfrac{r + 1}{l}$ 的形式。
但两次整除分块的复杂度是 $O(n^{\frac{3}{4}})$,考虑优化。
注意到第二次整除分块的式子为 $\sum_{t = 1}^{\lfloor\frac{n}{k}\rfloor}\lfloor\dfrac{n}{tk}\rfloor$,考虑变形为 $\sum_{t = 1}^{\lfloor\frac{n}{k}\rfloor}\lfloor\dfrac{\lfloor\frac{n}{k}\rfloor}{t}\rfloor$,此式即是 $\sum_{t = 1}^{\lfloor\frac{n}{k}\rfloor} d(\lfloor\frac{n}{k}\rfloor)$
而 $d(n)$ 为积性函数,意味着此式可以用筛法 $O(n)$ 求出来,所以说我们可以预处理出 $O(n^\frac{2}{3})$ 的指数,用数组存起来,对于这些,就可以不用整出分块,直接调用即可。
这样处理得到的复杂度可证是 $O(n^{\frac{2}{3}})$,足以通过此题。
B
题目简介
括号序列变形,当给出的左括号数量大于右括号数量时,可能成为括号序列(指向后添加括号能够形成合法括号序列)的数量。
题目分析
合法括号序列数量显然即是卡特兰数。
考虑用折现法分析,如果将左括号视为向右上走,右括号视为向右下走,那么不合法的方案即是会触及 $y = -1$ 的方案
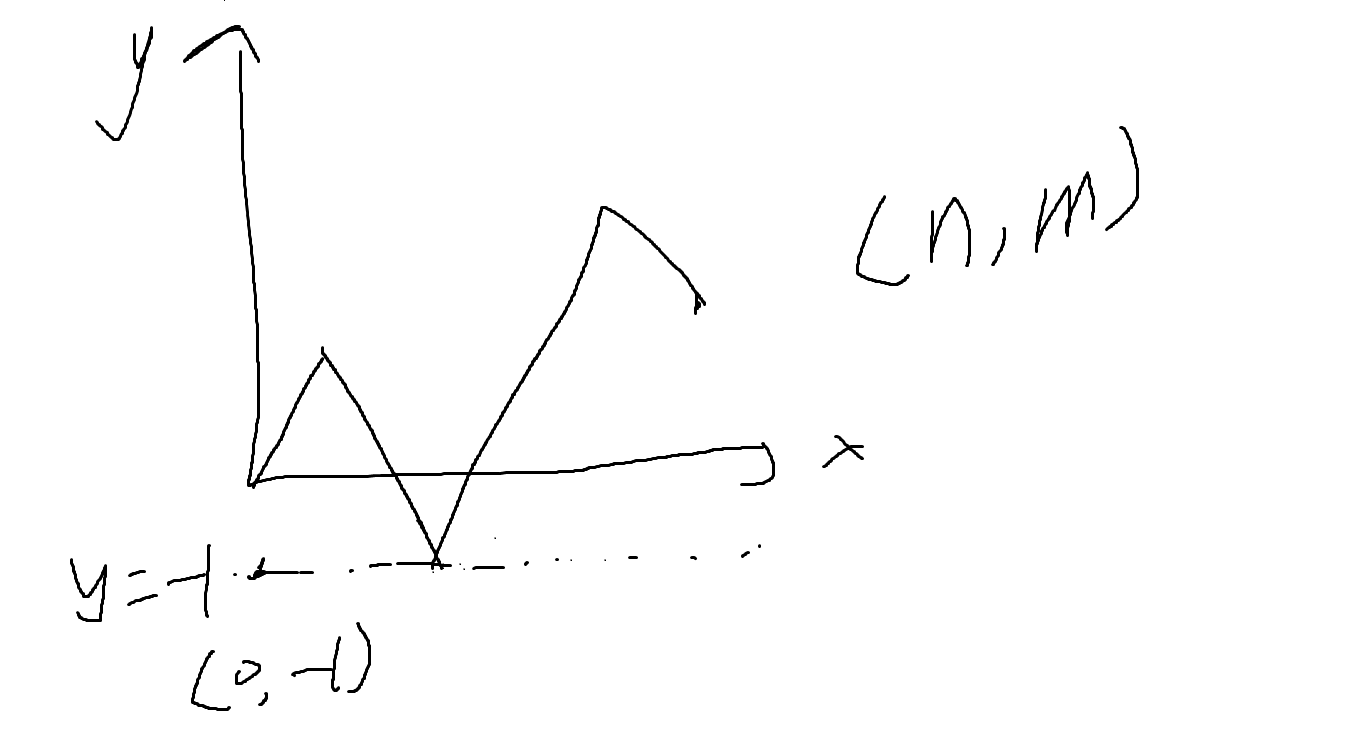
而此种情况下,显然可以将起点从 $(0, 0)$ 对称到 $(0, -2)$ 的位置,也就是说我们在不合法路径和从 $(0, -2)$ 到达 $(n, m)$ 的路径做到了一个一一映射关系。
利用容斥,其实就是总的方案数减去不合法的方案数。
而这些利用组合数都很好算出来。
总方案数为 $\binom{n + m}{n}$,不合法的方案数即是 $\binom{n + m}{n + 1}$,计算组合数相减即可。
C
题目简介
给你一个括号序列,询问将这个序列的某个真前缀移动到序列的尾部,能形成合法括号序列的方案数有多少种。
题目分析
真前缀的部分显然是可以枚举得到,关键是如何快速判断方案是否可行。
观察发现一个可行的方案,只要是真前缀作为后缀时可能被补充成一个合法的括号序列,且除去真前缀的后缀部分能够补充成一个合法的括号序列即可。所以我们可以对这两个分别考虑,看是否有一个点都满足这两个特性即可。
其实和用栈判断合法括号序列类似,以真前缀作为后缀是否可行来举例说明。
如果视右括号为 $+1$,视左括号为 $-1$,那么显然要求是,对一个序列,从后往前扫,需要每个位置的前缀和都大于等于 $0$,即是要求最小的前缀和大于等于 $0$。所以说我们可以从前往后枚举真前缀点的过程中,记录前缀和最小点即可。具体是当前为右括号时,意味着前缀和最小点会 $+1$;当前为左括号时,前缀和减少点会继续 $-1$,同时注意考虑当前点作为 $-1$ 是否可能称为前缀和最小点。如果当前点的前缀和最小点是大于等于 $0$ 的,则代表真前缀作为后缀是可行的。
而后缀作为前缀的处理方法类似。
这样就可以 $O(n)$ 解决这个问题了。
D
题目简介
$n$ 个物品,每个物品可以选择一个类型,分别可以获得 $a_i$,$b_i$ 的权重。$m$ 次询问,给定两个参数 $x_j, y_j$,代表有 $k_1x_j$ 的物品可以选择 $a$ 权重,有 $k_2y_j$ 个物品可以选择 $b$ 权重,且每个物品选且只选 $1$ 个类型,询问最终可以获得的最大权重为多少。
题目分析
首先我们很容易可以得到选择 $x$ 个 $a$ 属性的最大权重为多少,具体是假设我们一开始都选 $a$ 权重,然后将 $b_i - a_i$ 放入一个大根堆中,然后不断从堆中弹出计算即可。而且容易发现这是一个关于 $x$ 的单峰函数,而且峰点对应的 $x$ 值就是 $a_i$ 大于等于 $b_i$ 的个数,令这个数为 $d$。
而选择属性其实就是解一个方程 $k_1x + k_2y = n$,其中 $k_1 \ge 0 \land k_2 \ge 0$,即是找自然数解。显然就是一个 exgcd 的板子题。
根据 exgcd 的板子首先判断是否有一个自然数解。然后再让解出来的 $k_1x$ 成为第一个小于等于 $d$ 的值,再将这个答案与 $(k_1 + 1)x$ 比较一下,取最大值即可。
G
题目简介
给定 $n$,求
$$
\sum_{k = 1}^{n}\lfloor\sqrt{k}\rfloor \bmod 9998244353
$$
的值。
题目分析
化式子即可。
令 $a = \lfloor\sqrt{n}\rfloor$
$$
\begin{split} \sum_{k = 1}^{n}\lfloor\sqrt{k}\rfloor
&= \sum_{k = 1}^{a - 1}(k \times ((k + 1)^2 - k^2)) + (a \times (n - a^2 + 1))\
&= \sum_{k = 1}^{a - 1}(2k^2 + k) + …\
&= \dfrac{(a - 1)(a)(2a - 1)}{3} + \dfrac{a(a - 1)}{2} + (a \times (n - a^2 + 1))\
&= - \frac{1}{3}a^3 - \frac{1}{2}a^2 + (n + \frac{5}{6})a
\end{split}
$$
计算即可。
I
题目简介
给你 $n$ 个点,每个点有一个权重 $a_i$,你可以选择一个权重,然后计算 $\sum_{i = 1}^{n}(l_i + r_i)$,定义 $l_i$ 为 $i$ 左边第一个选择的权重,$r_i$ 为 $i$ 右边第一个选择的权重,若没有则为 0.
题目分析
显然,我们可以无脑将两端选择。
发现很容易可以写出 DP 方程,但写出后发现 DP 方程并不易优化,考虑换一个思路。
假设我们选择的集合是 $S$,那么我们的答案贡献可以记为
$$
W = \sum_{i = 1}^{|S| - 1}((S_{i + 1} - S_{i}) \times (a_{S_{i + 1}} + a_{S_{i}}))
$$
以 $i$ 为横坐标,以 $a_i$ 为纵坐标,发现这个式子含义即是代表一系列梯形的面积。而这个梯形的面积最大值显然是一个凸包,所以我们可以像斜率优化那样用栈维护即可。
具体是计算当前点与栈顶的斜率,如果大于了栈顶两个元素的斜率,就不断弹栈,并且将计算的答案减去。弹栈结束后,计算当前点和栈顶元素的贡献即可。
J
题目简介
FFT 板题
题目分析
学一下 FFT,将原来的两个函数转化为另一个表达方式 $O(nlog(n))$,然后再相乘 $O(n)$,然后还原 $O(nlogn)$ 即可。
K
题目简介
给你一个多重集 $S$,定义 $mex(S)$ 含义为最小的未出现在 $S$ 中的自然数。
你可以进行 $m$ 次操作,每次操作是选出当前 $S$ 的一个子集 $T$,可以是空集,然后求出 $mex(T)$,并且这个元素加入到 $S$ 中,求进行 $m$ 次操作后,可以形成的多重集有多少种。
题目分析
发现由于 $mex$ 运算的性质,如果每次都会生成一个新元素,那么这个元素的产生一定是递增的。
所以我们可以考虑枚举每次最多产生多少个新元素,不妨令这个值为 $k$,那么有 $0 \le k \le m \lor 1 \le k \le m$(取决于一开始的集合是否有 $0$ 元素)。
而对于每一个枚举的 $k$,首先我们假设已经添加了 $k$ 个新元素,也就是说剩下的 $m - k$ 次操作我们可以产生任意一个小于当前能产生的最大元素(这个可以预处理出来)。
假设这个最大元素为 $b$ 并且假设从 $0$ 到 $b$ 各自产生了 $a_i$ 次,那么有
$$
\sum_{i = 0}^{b}a_i = m - k (a_i \ge 0)
$$
而这也是一个典型的模型,这其实就是 $\binom{m - k + b + 1 - 1}{b + 1 - 1}$
所以预处理后,枚举这个 $k$ 计算即可。
M
题目简介
求满足 $\dfrac{an}{nb} = \dfrac{a}{b}$ 的 $(a, b, n)$ 的方案数。
满足 $1 \le a < A, 1 \le b < B, 1 \le n < N$
其中有 $1 \le A, B \le 10^5; 1 \le N \le 10^9$
题目分析
像题解一样推式子即可。
但好像给的题解是抄的洛谷题解,把错误也抄进去了(
最后应该令 $d^{\prime} = \dfrac{d}{\gcd(d, b^{\prime})}$,其余就没有问题了。
Q
题目简介
给你一个数组 $a_n$,对于所有 $(i, j, k, l) (1 \le i, j, k, l \le n)$,
令
$$
S = (a_i & a_j) \oplus (a_k | a_l)
$$
若有
$$
S \equiv 0 \pmod 3
$$
那么
$$
B += fib_{a_i & a_j} \times fib_{a_k | a_l}
$$
其中 $B$ 的初值为 $0$。
题目分析
考虑 FWT
首先容易发现 $(i, j)$ 和 $(k, l)$ 是互不干扰的,所以我们可以分别考虑。
对于 $(i, j)$,我们可以令 $c_i$ 表示元素 $i$ 在 $a$ 中的出现次数。
再令 $A_i = \displaystyle\sum_{j & k = i} c_j \times c_k$,$B_k = \displaystyle\sum_{j | k = i}c_j \times c_k$
这显然是一个 FWT 板子,然后对于每个 $A_i$ 和 $B_i$ 我们乘以一个相应的 $fib_i$。
此时我们再令 $C_i = \displaystyle\sum_{j \oplus k = i}A_j \times B_k$
也是一个 FWT 的标准形式
发现答案其实就是 $\sum[3 | i] \times C_i$
R
题目简介
求一系列的积性函数
$\varphi, \mu, \sigma_0, \sigma_1, (\mu \cdot \varphi) \ast \sigma_1$
含义分别是欧拉函数,莫比乌斯函数,因数个数函数,因数和函数。
题目分析
在欧拉筛的过程中计算即可。
这里就只考虑推到一下最后一个式子。
令最后一个式子为 $h$,
那么考虑 $h(p^k)$
根据迪利克雷卷积,
$$
h(p^k) = \sum_{d|p^k}\mu(d)\varphi(d)\sigma_1(\frac{p^k}{d})
$$
由于莫比乌斯函数的特殊性,有
$$
\begin{split}
h(p^k) &= \mu(1)\varphi(1)\sigma_1(p^k) + \mu(p)\varphi(p)\sigma_1(p^{k - 1})\
&= \dfrac{1 - p^{k + 1}}{1 -p} + 1 - p^k\
&= \dfrac{2 - p - p^k}{1 - p}
\end{split}
$$
线性筛这个式子,可以考虑用另一个数组将 $p^k$ 存起来用于递推即可。
T
题目简介
给你 $n$ 堆石子,每次你可以选择合并两堆石子或者从一堆石子取出一个。双方轮流进行操作,不能操作者输掉游戏。询问 $T$ 轮游戏中有几轮先手必胜。
题目分析
首先观察到总石子数是固定的,也就是说第二种操作数是固定的,$\sum_{i = 1}{n}a_i$ 次。
而第一种操作在第二种操作不影响石子总堆数的情况下也是固定的, $(n - 1)$ 次。
也就是说在这种情况下只需要判断奇偶性即可得到是否先手必胜。
但第二种操作事实上会影响到石子的堆数。
观察到在石子数量大于 $1$ 的堆数大于等于 $2$ 时,只有石子数量为 $1$ 的堆才会影响。
所以现在可以将每个状态抽象成两个属性:一是仅操作非 $1$ 堆可以操作的次数,二是 $1$ 堆的数量。发现这样状态数大大减少,记忆化搜索即可。
注意搜索过程中会有些转化即可。
V
题目简介
中国剩余定理板子
题目分析
像中国剩余定理一样构造解即可。
令 $A = \prod_{i = 1}^{n}a_i, A_i = \dfrac{A}{a_i}, B_i = inv(A_i, a_i)$
则对于每个 $a_i$,$ans = (ans + A \times B \times b_i) \bmod MOD$ 即可。
Y
题目简介
给你一个递推序列:
$$
a_{n + 1} = (k \cdot a_n + m) \bmod p
$$
其中,$k, m, p, a_0$ 已知,$p$ 为一个质数。
对于一个非负整数 $t$,询问是否存在一个非负整数 $i$,满足 $a_i = t$?
题目分析
当 $k = 0$ 时
有 $a_{n + 1} = m$
所以判断是否满足 $m = t \lor a_0 = t$ 即可。
当 $k = 1$ 时
有 $a_{n + 1} = a_n + m$,为一个等差数列
可化为 $a_n = a_0 + mn$,因为 $p$ 为质数,若 $m \ne 0$,显然能遍历所有剩余系。
所以判断是否满足 $m \ne 0 \lor a_0 = t$ 即可。
当 $k \ne 0 \land m \ne 1$ 时
有 $a_{n + 1} + \frac{m}{k - 1} = k(a_n + \frac{m}{k - 1})$,是一个等比数列的形式。
可得到
$$
a_n = (a_0 + \frac{m}{k - 1})k^n - \frac{m}{k - 1}
$$即是求是否存在一个 $n$ 满足
$$
\begin{gather*}
(a_0 + \frac{m}{k - 1})k^n - \frac{m}{k - 1} \equiv t \pmod p\
(a_0(k - 1) + m)k^n \equiv t(k - 1) + m \pmod p
\end{gather*}
$$即是一个标准的 BSGS 形式了,所以用 BSGS 判断即可。